2015年6月8日月曜日

MT4インジケータ ヒストリカルボラティリティ比率と東京時間レンジブレーク雑談

＃2016/2/4 HVとHV比率をFX-ONにアップしました。
http://mt4program.blogspot.com/2016/02/mt4_4.html

5/11に公開した「東京時間をぶっ壊せ！MT4で時間レンジブレイク向けインジケータを作ってみた。」が、ここにきてアクセス数が伸びてきました。公開当初はあまりアクセス数が無かったのですが、EGOISTさんやMorning_Limitedさんが、特定時間を狙った取引で利益をだしているので、同じような考え方でEURUSDのヨーロッパ時間開始直後で、もうけられないかを見分けるため注目を集めているようです。
ちょっとだけ見た目を変更した後続の記事もありますので、そちらもご確認ください。
「東京時間がもっとわかりやすくしてほしい。MT4レンジインジケータを改造してみた。」

私の調査結果では、ここ半年ほどはレンジブレークで有効そうに見えるけど、それ以上だと怪しいという感じです。いっそ14時と15時の値動きだけに着目して16時の1時間勝負したほうが勝率あるかも？調査した結果よければ、そのうちEAで出すかもしれません。

さておき、インジケータをまた作ってみました。
ヒストリカルボラティリティです。
ヒストリカルボラティリティとは、前回Close値/今回Close値比の標準偏差値です。
値動きがどのくらいあるのか？というのを判断するらしいです。

本来ならルート２０とかルート２５０とか掛けて、ある期間のボラティリティを出すための指標ですが、今回は短い期間のボラティリティと長い期間のボラティリティの割合をチャートにしてみました。裁量トレードの方はチャートを見ればすぐわかる！と思いますが、システム的に判定するために作ってみました。

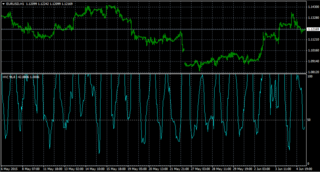
HV.PNG

EUR/USDの1時間足のボラティリティ比率です。お・・・見事に法則性がある感じで波打ってますね！って当たり前です。日本時間に対してヨーロッパ時間のボラティリティの方が高いっていう事を改めてグラフにしただけでした＾＾；；；；

短期の足に採用すると押し目や逆張りのタイミング測定に使えるかもしれません。また通常取引が多い時間帯でボラティリティが下がるということは、何か重要指標の発表があるかもしれないということを値動きから判定できるかもしれません。逆もしかりです。ただ、これだけでは明らかに材料不足です。ほかのインジケータと合わせて使用する形になるかと思います。

ソースコードはこちらから 
//------------------------------------------------------------------
// ヒストリカルボラティリティ比率

#property copyright "Copyright 2016,  Daisuke"
#property link      "http://mt4program.blogspot.jp/"
#property version   "1.00"
#property strict

#include 

#property indicator_separate_window
#property indicator_minimum    0
#property indicator_maximum    100
#property indicator_level1    50
#property indicator_levelcolor clrSilver
#property indicator_levelstyle STYLE_DOT

//バッファーを指定する。
#property indicator_buffers 2

//プロット数を指定する。
#property indicator_plots   1

//ヒストリカルボラティリティ
#property indicator_label1  "HV"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1

//差分
#property indicator_type2   DRAW_NONE

//入力パラメータ 期間
input int PeriodLong = 96;
input int PeriodShort = 8;

double hvBuffer[];
double diffBuffer[];

//------------------------------------------------------------------
//初期化
int OnInit()
{
   if( PeriodLong < 1 || PeriodLong <= PeriodShort ) return (INIT_PARAMETERS_INCORRECT);
   
   //インジケーターバッファを初期化する。
   SetIndexBuffer(0,hvBuffer);
   SetIndexBuffer(1,diffBuffer);
   
   SetIndexDrawBegin(0, PeriodLong + 1);
   
   string short_name = "HV( " +  IntegerToString(PeriodLong) + "," + IntegerToString(PeriodShort) + " )";
   IndicatorShortName(short_name);
   
   return(INIT_SUCCEEDED);
}


//------------------------------------------------------------------
//計算イベント
int OnCalculate(const int rates_total,          //各レート要素数
                const int prev_calculated,      //計算済み要素数
                const datetime &time[],         //要素ごとの時間配列
                const double &open[],           //オープン価格配列
                const double &high[],           //高値配列
                const double &low[],            //安値配列
                const double &close[],          //クローズ価格配列
                const long &tick_volume[],      //ティック数（要素の更新回数）
                const long &volume[],           //実ボリューム（？）
                const int &spread[])            //スプレット
{
   //元となる値を計算する。
   for( int i = (rates_total - prev_calculated - 1); i>=0 ; i-- )
   {
      if( i >=  rates_total - 3 )
      {
         diffBuffer[i] = 0 ;
         continue;
      }
      diffBuffer[i + 1] = MathLog(close[i + 1] / close[i]);
      double longStd = StdDev(diffBuffer, PeriodLong, i + 1);
      hvBuffer[i] = (longStd != 0 ? (StdDev(diffBuffer, PeriodShort, i + 1) / longStd) : 0) * 100;
   }
   return(rates_total - 1);
}

//------------------------------------------------------------------
//標準偏差を求める。
// return 標準偏差
double StdDev( 
   const double &values[],      //元となる配列
   int count,                   //計算対象数
   int shift                    //シフト
)
{
   if( (count + shift) > ArraySize(values) ) return 0;

   double avg = 0 ;
   double mu = 0 ;
   for( int i = shift; i < shift + count; i++ )
   {
      avg += values[i];
   }
   avg = avg / count;
   
   for( int i = shift; i < shift + count; i++ )
   {
      mu += MathPow(values[i] - avg, 2);
   }
   
   // 標準偏差
   return MathSqrt(mu / count);
}


ラベル: