単純移動平均は遅れているため、シグナルとして使用すると判断が遅くなることを、前回の記事で検証しました。では単純移動平均は使わない方がよいのでしょうか?いいえ。単純移動平均には、その傾きによってトレンドを推測できるという重要な役割があります。ちょっとした数学を使って検証したいと思います。
移動平均といっても、さまざまな種類があります。
有名どころで、単純移動平均(SMA)、加重移動平均(WMA)、指数平滑移動平均(EMA)とありますよね?皆様どれを使っていますか?
単純移動平均以外の特徴は次の通りです。
・加重移動平均:少ない遅延で平滑化する。
・指数平滑移動平均:単純と加重の中間。
単純移動平均と比較して、同じ遅延であれば加重/指数の方が滑らかだし、同じ滑らかさであれば加重/指数の方が遅延が少ないという事になります。移動平均を使う主目的の平滑化では、加重/指数を使う方が理に適っているということになります。
では単純移動平均はお役御免でしょうか?
いいえ。単純移動平均にはとても重要な役割があります。トレンド方向を判別することです。
分かりやすくするためにEXCELグラフで視覚化したいと思います。
■正弦波に対して移動平均をとる
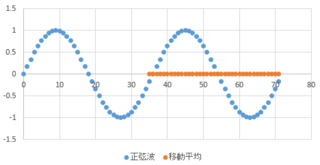
これは、正弦波形に対して波長と同じ長さの移動平均をとったグラフです。波形成分が打ち消されて移動平均は0となっています。このようにある波長と同じ期間の単純移動平均をとると波形成分による振幅を取り除くことができます。この特性を利用すると、小さい周期の値動きを排除してトレンドの方向をつかむ事ができそうです。
もう一個わかりやすい例として、一定値を加えて生成した正弦波に対して、移動平均をとった結果をしめします。
■線形増分を持つ正弦波に対して移動平均をとる
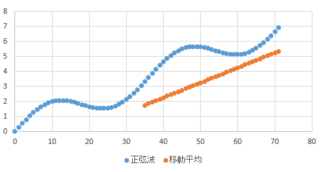
正弦波波形成分が取り除かれてトレンドラインが表れている様子がよくわかります。
上記結果から、単純移動平均はチャートに存在する短期波長成分の揺らぎを排除してトレンドの方向を知るのに非常に重要なツールであることが示されています。
さて、ここで問題があります。単純移動平均を使用してトレンドを得る為には、取り除きたい波形成分の波長が必要です。ここで移動平均の期間としてよく使われる21という数字は数学的に正当性がある数字なのでしょうか?チャートの波長成分を分析するオシレータを使用した結果です。
■EURUSD 1時間足 主要波長解析
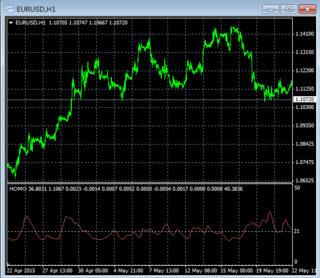
これを見ると21付近をうろうろしています。みんなが21を使うからかどうかはわかりませんが21という数字にはそれなりの数学的根拠がありそうです。
ということで、単純移動平均は遅延が大きいため売買シグナルを図るツールとしては使用が難しいですが、その傾きはトレンド方向を知る重要なツールであることが判りました。
なんとなくで移動平均を使っていると、その使用法に勘や経験に頼る事になりますが、このように数学的に説明すると利用シーンがはっきりするなぁと思っていますが皆さんどうですか?